Bayesian Methods in Data Science

In the ever-evolving field of data science, where uncertainty is a constant companion and decisions must often be made with incomplete or noisy information, Bayesian methods stand out as a robust and flexible framework for reasoning, prediction, and inference. Unlike traditional frequentist approaches, which rely on long-run frequencies and fixed parameter estimates, Bayesian methods embrace a probabilistic mindset—integrating prior knowledge, updating beliefs with new evidence, and offering a nuanced view of uncertainty. This adaptability has made Bayesian techniques indispensable across diverse domains, from healthcare and finance to marketing and cutting-edge machine learning applications.

The stakes are high in today’s data-driven world. According to a 2021 report by the International Data Corporation (IDC), the global datasphere is expected to balloon to 175 zettabytes by 2025. This explosion of data brings both opportunity and complexity, demanding sophisticated tools to extract meaningful insights from high-dimensional, uncertain environments. Bayesian methods, with their ability to model uncertainty explicitly and incorporate domain expertise, are uniquely equipped to meet this challenge. Whether you’re a data scientist looking to refine your analytical toolkit, a business leader striving for smarter decisions, or a researcher tackling intricate problems, mastering Bayesian methods is a critical step toward thriving in the modern data landscape.

This blog post provides an in-depth exploration of Bayesian methods in data science. We’ll unpack the foundational principles of Bayesian thinking, dive into key techniques like Bayesian inference and Markov Chain Monte Carlo (MCMC), and showcase real-world applications that highlight their practical power. By the end, you’ll understand why Bayesian methods are not just a statistical novelty but a strategic asset for addressing uncertainty and complexity in data science.

The Bayesian Paradigm: A New Lens on Probability

Bayesian methods rest on a distinctive philosophy of probability and inference that sets them apart from frequentist statistics. While frequentist approaches define probability as the long-term frequency of events and treat parameters as fixed (though unknown) values, Bayesian statistics interprets probability as a measure of belief or confidence in an event or parameter. This perspective enables Bayesian methods to weave prior knowledge into the analysis and refine that knowledge as new data emerges.

Core Concepts in Bayesian Thinking

To harness the power of Bayesian methods, it’s essential to understand a handful of foundational concepts:

1. Prior Probability

The prior probability reflects our initial belief about a parameter before observing any data. This could stem from historical trends, expert insights, or even an educated guess. For example, if we’re estimating the likelihood of a customer abandoning an online shopping cart, we might use last month’s abandonment rate as our prior.

2. Likelihood

The likelihood measures the probability of observing the data given a specific parameter value. It evaluates how well a hypothesized parameter explains the evidence at hand. In the cart abandonment scenario, the likelihood would assess how plausible the observed customer actions are under a given abandonment probability.

3. Posterior Probability

The posterior probability is our updated belief about the parameter after incorporating the data. It’s derived using Bayes’ theorem, the cornerstone of Bayesian analysis:

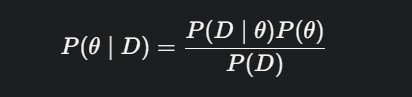
Where:

P(θ∣D) P(\theta \mid D) P(θ∣D) is the posterior probability of parameter θ \theta θ given data D D D,
P(D∣θ) P(D \mid \theta) P(D∣θ) is the likelihood,
P(θ) P(\theta) P(θ) is the prior,
P(D) P(D) P(D) is the marginal likelihood (a normalizing factor ensuring the probabilities sum to 1).

This equation captures the essence of Bayesian reasoning: beliefs evolve dynamically as evidence accumulates.

4. Credible Intervals

Unlike frequentist confidence intervals, which can be tricky to interpret, credible intervals offer a straightforward probabilistic statement. A 95% credible interval, for instance, indicates a 95% probability that the true parameter value lies within that range, given the data and prior.

Why Bayesian Methods Shine in Data Science

Bayesian methods bring a suite of advantages that align seamlessly with the demands of data science:

1. Mastering Uncertainty

Data science often grapples with uncertainty—whether predicting stock prices, diagnosing diseases, or forecasting demand. Bayesian methods excel here by delivering a full probability distribution over outcomes, rather than a single, potentially misleading point estimate.

2. Leveraging Prior Knowledge

In fields rich with historical data or expert insight, Bayesian methods allow this prior knowledge to be systematically folded into the analysis. This is a game-changer in scenarios with sparse data, where traditional methods might falter.

3. Modeling Flexibility

Bayesian approaches can tackle intricate, hierarchical models that frequentist techniques struggle to estimate. This versatility is vital for capturing the layered complexity of real-world systems.

4. Continuous Learning

Bayesian methods are inherently sequential: today’s posterior becomes tomorrow’s prior as new data arrives. This makes them ideal for adaptive applications like real-time analytics or online learning systems.

Essential Bayesian Techniques in Data Science

Bayesian methods encompass a rich array of tools, each suited to specific challenges. Here’s a look at some of the most impactful techniques:

1. Bayesian Inference

Bayesian inference is the process of refining beliefs about parameters or hypotheses based on data. It underpins countless applications, from A/B testing to tuning machine learning models.

Example: In A/B testing, Bayesian inference can calculate the probability that one webpage design outperforms another, offering a direct, decision-ready answer instead of relying on abstract p-values.

2. Markov Chain Monte Carlo (MCMC)

When posterior distributions are too complex for analytical solutions, MCMC methods—like Metropolis-Hastings or Gibbs sampling—step in. These algorithms approximate the posterior by drawing samples from it, making them indispensable for high-dimensional or hierarchical models.

Use Case: MCMC powers Bayesian neural networks, where the sheer number of parameters defies traditional computation.

3. Bayesian Networks

Bayesian networks use directed acyclic graphs (DAGs) to model conditional dependencies among variables. They streamline the computation of joint probabilities and excel in probabilistic reasoning.

Application: In diagnostics, Bayesian networks can link symptoms, diseases, and risk factors to support clinical decision-making.

4. Gaussian Processes

Gaussian processes (GPs) provide a non-parametric Bayesian approach to regression and classification. They model functions flexibly and quantify prediction uncertainty, making them perfect for tasks like time series analysis.

Example: GPs are a go-to method for hyperparameter optimization in machine learning, balancing exploration and exploitation.

5. Variational Inference

Variational inference (VI) offers a faster alternative to MCMC by reframing inference as an optimization problem. It’s scalable and efficient, particularly for large-scale data.

Use Case: VI drives applications like topic modeling (e.g., Latent Dirichlet Allocation) and Bayesian deep learning (e.g., variational autoencoders).

Real-World Impact of Bayesian Methods

Bayesian methods are far more than academic exercises—they deliver tangible value across industries. Here are five compelling examples:

1. Healthcare: Personalized Medicine

Bayesian approaches personalize treatments by integrating patient data—genetics, history, and trial outcomes. Bayesian adaptive trials, for instance, adjust dynamically as data accrues, enhancing efficiency and patient care.

2. Finance: Risk Management

Banks and insurers use Bayesian models to evaluate credit risk, detect anomalies, and optimize investments. By blending prior market knowledge with real-time data, these models outpace traditional risk assessments.

3. Marketing: Customer Insights

Bayesian clustering, such as Gaussian mixture models, segments customers with precision, accounting for uncertainty in group assignments. This yields actionable, nuanced marketing strategies.

4. Machine Learning: Hyperparameter Tuning

Bayesian optimization leverages Gaussian processes to fine-tune machine learning models efficiently, cutting the computational cost of exhaustive grid searches.

5. Natural Language Processing: Topic Discovery

Bayesian techniques like Latent Dirichlet Allocation (LDA) uncover latent themes in text corpora, enhanced by priors on word distributions for richer insights.

Challenges in Bayesian Methods

Despite their strengths, Bayesian methods pose challenges that practitioners must address:

1. Computational Demands

MCMC and similar methods can be resource-intensive, especially for large datasets or intricate models. Modern hardware and algorithms are easing this burden, but it’s still a factor.

2. Prior Sensitivity

Selecting priors is a delicate balance. Overly strong priors can skew results, particularly with limited data. Sensitivity analyses and neutral priors can mitigate this risk.

3. Interpretability

Complex Bayesian models can be hard to explain, especially to non-technical stakeholders. Visualization tools like posterior plots help, but clarity remains a hurdle.

4. Scalability

Traditional Bayesian inference may falter with massive datasets. Innovations like variational inference and stochastic MCMC are scaling solutions to meet big data needs.

Best Practices for Bayesian Success

To wield Bayesian methods effectively, follow these guidelines:

1. Start Small

Begin with simple models (e.g., conjugate priors) to grasp Bayesian mechanics before scaling up to complex challenges.

2. Choose Priors Wisely

Use domain knowledge for informative priors when justified, but opt for weakly informative priors in data-rich settings to let evidence dominate.

3. Validate Thoroughly

Perform posterior predictive checks—comparing observed data to simulated predictions—to ensure model fit and refine as needed.

4. Highlight Uncertainty

Leverage the full posterior distribution, reporting credible intervals to capture the range of possibilities, not just point estimates.

5. Tap Modern Tools

Libraries like PyMC3, Stan, and TensorFlow Probability streamline implementation, letting you focus on modeling rather than computation.

The Future of Bayesian Methods

Bayesian methods are set to grow in influence as data science advances. Key trends include:

Deep Learning Synergy: Bayesian neural networks and variational methods are merging probabilistic rigor with deep learning’s power.
Big Data Scalability: Approximate inference techniques are unlocking Bayesian potential for massive datasets.
AutoML Integration: Bayesian optimization is fueling automated machine learning, enhancing model efficiency.
Causal Insights: Bayesian networks are advancing causal inference, offering a probabilistic lens on cause and effect.

These shifts will broaden Bayesian methods’ reach and impact.

Conclusion: Bayesian Thinking as a Data Science Superpower

Bayesian methods provide a principled, powerful framework for navigating the uncertainties and complexities of data science. From healthcare breakthroughs to financial precision, their applications are vast and profound. Though challenges like computation and prior selection persist, the rewards—flexibility, uncertainty quantification, and knowledge integration—make them a vital tool for today’s data scientist.

Adopting Bayesian methods is more than learning techniques; it’s embracing a mindset. In a world awash with data yet starved for certainty, Bayesian thinking offers a clear path forward. Let it guide your next analysis—and watch your insights deepen.